スイングの慣性モーメント
当サイト筆者は、ゴルフ理論でクラブ選定方法、製造方法として振動数理論並びに重量管理理論を提案、平成元年に発明その後、日本で初めて特許を平成６年に取得（第２５９７７８９号）、富士通FMRシリーズゴルシスとして、大手ゴルフクラブメーカブリヂストンスポーツや、大手シャフトメーカに情報提供、この分野においてはパイオニアとして貢献してまいりました。その資料を基に当サイトは構成されています。
スイングの慣性モーメント
これまで慣性モーメントという言葉がよく出てきます。ゴルフのスイング理論やシャフト理論を語る上で慣性モーメントの重要な要素の一つだという事を理解してください。
運動（物の動き）には直線運動と回転運動の２つに分類できます。これらの物理的諸要素を対比すると以下の表になります。
直線 |
運動 |
回転 |
運動 |
|---|---|---|---|
質量 |
ｍ |
慣性モーメント |
I |
速度 |
ｖ＝ｘ’ |
角速度 |
ｗ＝θ’ |
加速度 |
α＝ｘ’’ |
角加速度 |
θ’’ |
運動量 |
ｍｖ |
角運動量 |
Iｗ |
運動エネルギー |
１２ｍｖ² |
回転エネルギー |
１２Iｗ² |
力 |
ｍｘ’’ |
トルク |
N＝Iθ’’ |
この直線運動とゴルフスイングのような回転運動の間には対比した関係があります。
直線運動の質量、これは物を動かすときの重さと考えてよいのですが、これが回転運動の場合は慣性モーメントになります。
つまり、慣性モーメントは物体を回転させるときの重さと考えてください。
言いかをかえると直線運動で物を動かすときの重さとして質量に対して、回転では回転のしにくさとしての慣性モーメント、また直線運動の速度に対して回転運動の角速度、運動量にたいしては角運動量、よく知られる運動エネルギーが「１/２ｍｖ²」に対して回転エネルギーは「１/２ｌｖ²」、力はトルクと両者は完全に対応することができ、置き換えて考えることができます。
ゴルフにおける運動量と言えばボールの弾道のような放物運動のような特殊なものを除きほとんどが回転運動になります
従って、慣性モーメントはゴルフのスイングや道具を考察するのに必要な概念となる訳です。
簡単な例で図を参考にいしてください。
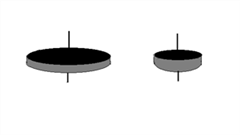
この２つのコマは同じ２００ｇで大きさの異なったものです。これらのそれぞれを回すとき同じ力で同じように回すことが出来るでしょうか。
答えは右のコマの方が左より少ない力で回すことができます。
これは回転の中心から外側に重さがあれば慣性モーメントが大きく働き、より大きな力が必要になるからです。
慣性モーメントを最大限にするスイング
次にスイングを図に示すようなツーバーシステム（Two Lover System)と仮定します。
グーグルとその情報提供者
求めようしているのは左肩を回転の中心として左腕とクラブの二つのレバーからなるシステムの慣性モーメントです。
現実のスイングでは回転の中心が若干横移動するため、この例は少し異なりますが計算や説明が複雑になるためこのモデルで説明します。
スイングが回転運動であるため投入エネルギーをE、スイングの回転速度をｗ、とすると次の式が得られます。
E=１/２Iｗ² ここではIは慣性モーメントになります。
この式からスイングの速度、つまり回転速度ｗを最大にするにはｗ²＝２E/Iとなり、慣性モーメントを最小にしなければならないことがわかります。
つまり、慣性モーメントを最小にするには回転中心に、出来る限り質量を集中させればよいわけです。
具体的にいえば、上の写真のLの距離を短くする、つまり左肩とシャフトの作る角度θを最小にすればいいわけです。
ダウンスイング中クラブが体に巻きつくようなスイングをすれば良いことになります。つまり、ダウンスイングでは右肘が伸びてはいけないことになります。
このようにダウンスイング中のリスト角（ダウンコック）を小さく保持することは、スイングの教えにいわれるタメという概念と一致します。
タメはスイング中のエネルギーを溜めて、インパクト前でこれを一気にリリースするということで、レート、ヒッテング、つまり遅らせて打つと表現しています。
いずれにせよ、ダウンスイングでトップスイングでのリスト角を出来る限り遅くまで保持しておくということで、これを科学的に解釈すると、スイングシステムのおける慣性モーメントをダウンスイング中に小さく保持することと結論づけられます。
すると先に示した理論によって当然スイングの回転速度は上がるというわけです。
フィギア―スケートで回転をしている時、両手を広げて回転しているとき、手を上げているときでは回転速度が違うのはこの理由からです。
関連記事
|
楽天ゴルフ
|
アトミックゴルフ | ||
|---|---|---|---|
|
|
|
|
|---|
ゴルフクラブ |
|
|---|---|
|
|
|
|
|
|
ウエアー |
|
|---|---|
|
|
|
|
|
シューズ |
|
|---|---|
|
|
|
|
|
|
| バッグ・グローブ・ボール・その他 | のアイテム |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
人気の新作クラブ・シューズ・ウェア・バッグ・グローブ・ボール・ゴルフナビなどが大集合！レディース・メンズ・子供用も品数豊富に取り揃え。口コミ・ランキング・各種特集ページから簡単にお選びいただけます。
#スイングの慣性モーメント記事一覧
スイングと角運動量理論
スイングの角運動量を増やすスイング中の角運動の推移角運動と左サイドの壁当サイト筆者は、ゴルフ理論でクラブ選定方法、製造方法として振動数理論並びに重量管理理論を提案、平成元年に発明その後、日本で初めて特許を平成６年に取得（第２５９７７８９号）、富士通FMRシリーズゴルシスとして、大手ゴルフクラブメーカ...
#スイングのスピードの加速は回転軸【スイング軸】
ゴルフ上達の基本は回転軸【スイング軸慣性モーメントを生かす小さい回転軸【スイング軸】回転軸【スイング軸】とスイング軌道トップ、ダフリなどのミスショットのリスクを下げるシンプルに回転軸【スイング軸】を作る当サイト筆者は、ゴルフ理論でクラブ選定方法、製造方法として振動数理論並びに重量管理理論を提案、平成...
