ヘッドとボールのミート係数【反発特性】
![]()
![]()

当サイト筆者は、ゴルフ理論でクラブ選定方法、製造方法として振動数理論並びに重量管理理論を提案、平成元年に発明その後、日本で初めて特許を平成6年に取得(第2597789号)、富士通FMRシリーズゴルシスとして、大手ゴルフクラブメーカブリヂストンスポーツや、大手シャフトメーカに情報提供、この分野においてはパイオニアとして貢献してまいりました。その資料を基に当サイトは構成されています。
ヘッドスピードとボール反発特性(ミート率)
図は質量Mの物体(クラブヘッドと考える)が静止している質量mの物体(ボールと考える)に衝突する時のものとします。
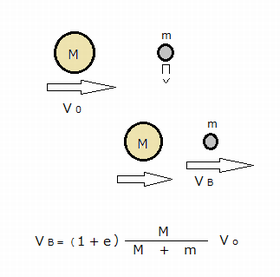
ここで、Vo , Vbはそれぞれの衝突前のクラブヘッドの速度、及び衝突後飛び出すボールの初速度です。
この比、Vb/Voの大きいものが反発が良いということになります。
ここでeの値は、これは反発係数と呼ばれているものであり、その大きさは0~1の間です。
これは、エネルギーの損失の程度を示す尺度で、e=0とは、最もエネルギー損失の場合で、e=1はエネルギーの損失のない場合です。

e=0の場合
この場合、完全非弾性衝突と呼ばれ、クラブとボールは反発しない。これは、ちょうどボールが粘土でできている場合です。
インパクトでボールは反発しないでクラブと一緒にくっいて、そのまま運動する状態です。
ここで、ヘッド重量200g、ボールが46gとして理論式に代入するとVb/Vo=0.81になります。
ボールの初速はヘッドスピードより遅いため、ボールは反発しなくなります。

e=1の場合
この場合、完全弾性衝突と呼ばれ、クラブヘッドとボールの反発が一番良い状態です。
この時、Vb/Vo=2×0.81=1.62で、先の場合の二倍になります。
つまり、入射してきたクラブヘッドの1.62倍の速度で飛び出すことになります。
このVb/Voのことをゴルフ業界ではミート率と呼ばれ、この値が高い程ボールの反発は良く、ボールは良く飛ぶことになります。
ところが、実際にドライバーを用いた実験を行うとミート率は1.5ぐらいの結果しかでず、完全弾性帯の1.6よりかなり低い値になります。
クラブヘッドは硬い金属なので完全弾性体とみなしても、ボールはそう見なせないことになります。
ミート率1.5を代入して見ればe=0、85となり15%程度は非弾性の要素がボールに含まれていることになります。
しかし、この計算にはボールの変形が考慮されていません。
そこで、ゴルフボールの質量mの質点とバネ定数Kの実験モデルで考えてみます。
このモデルでインパクト前半はボール自体のバネ効果でボールは押しつぶされ、後半では、このこのスプリングが伸びる事で、ボールはヘッドを蹴って飛び出します。
つまり、反発して飛び出すというメカニズムになります。

このボールの圧縮し、伸長するのを一種の振動とみなすと、この質点mとバネ係数Kからなる固有振動数は2π√K/Mで表せます。
ボールにはコンプレッション値と言う硬さを表す尺度があり、Kがこれに当たります。
つまり、コンプレッション値の高い、硬いボールは固有振動数が高く、飛び出しも速いことになります。
逆に、コンプレッション値の低いボールは軟らかくゆっくりっしている。
これらを、球離れが「速い」「遅い」と表現します。
ボールはこのように、ヘッドから振動で飛び出し、ボールの初速は、この振動による速度と、その時のヘッドスピードの和になるのです。
この様にして、理論的に前記ミート率を計算すると Vb/Vo=1.54 となります。
|
|
|
|---|---|
|
|
ブランド別ゴルフクラブはこちらから
メーカ別シャフト装着はクラブこちらから

ゴルフジャンル一覧と売れ筋ランキング
ゴルフクラブ |
|
|---|---|
|
|
|
|
|
|
ウエアー |
|
|---|---|
|
|
|
|
|
シューズ |
|
|---|---|
|
|
|
|
|
|
| バッグ・グローブ・ボール・その他 | のアイテム |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
人気の新作クラブ・シューズ・ウェア・バッグ・グローブ・ボール・ゴルフナビなどが大集合!レディース・メンズ・子供用も品数豊富に取り揃え。口コミ・ランキング・各種特集ページから簡単にお選びいただけます。
ラウンド中のコース戦略のための対応やクラブ選択についての情報
![]()
![]()









