シャフト振動数の定義
![]()
![]()

当サイト筆者は、ゴルフ理論でクラブ選定方法、製造方法として振動数理論並びに重量管理理論を提案、平成元年に発明その後、日本で初めて特許を平成6年に取得(第2597789号)、富士通FMRシリーズゴルシスとして、大手ゴルフクラブメーカブリヂストンスポーツや、大手シャフトメーカに情報提供、この分野においてはパイオニアとして貢献してまいりました。その資料を基に当サイトは構成されています。
飛距離アップにはヘッドスピードにシャフトの硬さ(振動数)を更に分析シャフトの再現速度を割り出し一致させることが最も飛距離アップや方向の安定性が計れます
それは、ヘッドスピードとシャフトの硬さ(振動数)が一致したシャフトからは、最大のボール初速と大きな慣性力と遠心力がボールに伝わり、飛距離を伸ばせ正確なショットを打つことができるからです。
シャフトのシャフトの振動数理論で飛距離アップ
シャフト振動数
振動数(しんどうすう、英語:frequency)は、物理学において等速円運動あるいは単振動などの振動運動や波動が単位時間当たりに繰り返される回数になります。振動数は、運動の周期の逆数であり、単位はヘルツになります。
振動の速さは単位時間に起こる往復運動の回数で表され、この回数を振動数または周波数といい単位はHz(ヘルツ)になります。
角振動数
振動の1回の往復運動は円運動1周に対応していて、振動の速さは単位時間におこなわれる円運動の回転角で表されこれを角振動数といいます。
角振動数は振動数に1周の角度2π(rad)をかけて定義される。単位はrad/sになります。
この角運動は、アドレスで構えた前傾姿勢の分、地面に対して角度を持ったスイング軌道の中で生じる固有振動数を意味します。

ゴルフシャフトの振動数を波形に置き換え解説
振動数をゴルフクラブのシャフトの硬さに適応するには、振動数を深堀して理解することが重要です。
シャフトの振動数は上に示すように、単位時間当たりに繰り返される回数であって、一般的なシャフトの硬さ表示Rに置き換えればRの表示を細かく割れば済むことになります。
但し、振動数は、一般的なシャフトフレックス、S,Rの静止的硬度でなく、実際のスイング中のシナリ戻りの速度になります。
ここで重要な点は、シャフトが等速運動であれば、シャフトの繰り返される運動を時間に置き換えることができることです。
つまり、シャフトの硬さを時間に置き換えが可能になることで、シャフトのシナリ速度を時間で表すことができるのです。
このシャフトのシナリ速度こそがシャフト復元速度に置き換えることができ、インパクトのタイミングでスイングで最も重要なファクターになるのです。
![]()
そこで、具体的に詳細な説明が以下の記事になります。
ゴルフシャフト振動測定器を使い、実際シャフトがスウイングしている状態の、シャフトの硬さを数値化した値が振動数(cpm)になります。
この振動数(CPM)の持つ意味は、シャフトが1分間に何回ヘルツ【上下動】運動を起したかの回数の数値です。
振動数(cpm)はCycie Per Minuteの略
ゴルフスイングの場合は、角振動でシャフトの振動数1ヘルツ(1回)が1回のスイングにあたり、この時のシャフトの速さ(往復するスピード)と、ヘッドスピードの値と一致させることで、両方のエネルギーが合体して、相乗効果で直接飛距離アップと正確なボールを打つのに決定的な役割をします。
振動数とヘッドスピードの一致は、正しいスイングを作る上でとても大切な要素で、シャフトのタイミングがスイング(ヘッドスピード)と合うことで、理想にスイングを行えることになるからです。を作ると言われる所以です。
そこで、シャフト振動数の定義を最低理解しておくのは、シャフトの振動は固有(等速)であるということです。
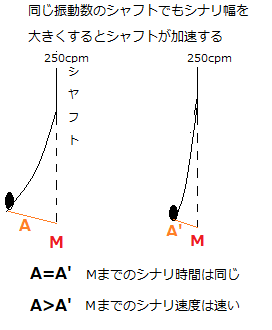
この固有振動は下の図で示すように、250cpmのシャフトが同じ長さでは負荷をかけた場合で起こる、ふり幅の大きさや小ささで振動数は変化しないことです。

スイング中のシャフトのふり幅が違ってきても、インパクトのタイミング(復元する時間は同じ)は変化しないことです。
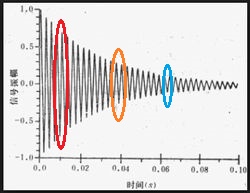
以下の表は、1本のシャフトに負荷をかけた場合の、シャフトのシナリを時間帯で表したヘルツになります。
表から赤 大きく振れている オレンジ 普通の振れ 水色 減速した振れ で見られるように、縦のシナリ幅は時間とともに小さく変化しますが、横軸のシナリ速度(シナリ時間)には変化が見られないことです。
この横軸のシナリ速度が、そのシャフトの持つ固有のシナリ速度、インパクトの時間でもあります。
シャフトの硬さ |
シャフト復元時間 |
タイミング |
適合 |
|---|---|---|---|
240cpm |
0.0625秒 |
遅い |
|
250cpm |
0.06秒 |
||
260cpm |
0.057秒 |
速い |
上の表から、各3本のシャフトは異なった振動数で、復元時間も異なります。真ん中の250cpmを基準にすれば、260cpmは250cpmに比べインパクトのタイミングが速く、240cpmは250cpmに比べインパクトのタイミングが遅いことを表しています。
さらに、このシャフトのタイミング(シャフトの復元時間)はヘッドスピードを変えても不変で、これが固有振動数の定義になります。
上の振動波動の図から分かるように、縦のシナリ幅は時間とともに小さく変化しますが、横軸のシナリ速度(時間)には変化が見られないことです。
例えば、硬いシャフトを柔らかくしならせようと、無理やりヘッドスピードを上げてもシャフトのシナリ戻りの時間は変化しないと言うことです。
下の振動数を電気信号ヘルツに変換図で説明すると、250cpmのシャフトのA~A’の時間帯は、ヘッドスピードが変化しても変わらないことです。
固有振動理論から、1本のシャフトの復元時間はふり幅の大きさで変化は起こさなことです。ただし、ふり幅が大きい方インパクト時の衝撃度が高まることから、ダウンスイングはレートヒッテングでシャフトのシナリを大きく作る方か飛距離を伸ばせることになります。
シャフトの固有振動数は、シャフトの動的な動きの硬さで(cpm)スイングにおけるインパクトのタイミングと定義づけることができます。
異なるシャフトの振動数それぞれでインパクトのタイミングが異なって来ることが定義できるのです。
この理論が固有振動数理論で以下の記事を読む上で必ず頭に入れておいてください。
![]()
![]()
振動数をヘルツに変換/インパクトのタイミング時間を割り出す
下の図は、振動数を電気信号に置き換えた1ヘルツの表示図です。
測定値は一分間に何回の振動を起こしたかの値ですが、スイングにおいては、1回のサイクルでアドレスからフィニッシュまでが行われます。
上の図の解説
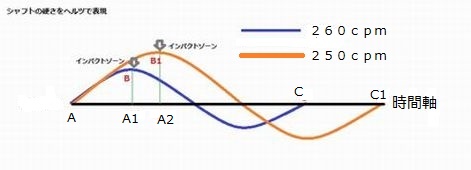
上の2本の曲線は、異なった硬さを持つ2本のシャフトの振動数の値を1ヘルツに置き換えた図で表示しています。
Aの横軸は時間値で、青の曲線はシャフトの硬さが260cpmの1ヘルツを表しています。、オレンジの曲線は250cpmの1ヘルツの状態を表しています。
A-Cは青のシャフトのシナリ速度(時間)、A-C1はオレンジのシャフトのシナリ速度(時間)になります。横軸が時間を示すことで、青のシャフトがオレンジのシャフトよりシナリ時間が速い事がわかります。これは青シャフトがオレンジシャフトより硬いことを意味します。
この青並びにオレンジの曲線を、スウイング中の位置に対比させると、Aは青、オレンジシャフトが共にトップスイング状態で、シャフトのシナリが発生した瞬間の位置になります。
A~A1、A~A2がダウンスウイングの時間帯になり、Bは青シャフトのインパクトの時間帯、B1がオレンジのシャフトのインパクトの時間帯になります。
このA1は青のシャフトの最下点に当たりシャフトが最もエネルギーを貯めるジャストタイミングの地点になります。同様、B1はオレンジシャフトの最下点ジャストタイミングに当たりシャフトが最もエネルギーを貯める地点になります。
「シャフトの最下点はシナッタシャフトが元の状態に復元する最もエネルギーを多く蓄えた地点になります」
そこで、波長とはシャフトのシナリ速度(時間)で、波高はシャフトのシナリ幅と理解してください。
Aからの横軸は時間を表していますから、青曲線のA~C オレンジ曲線のA~C1は波長になり、シャフトの1回の上下動の復元時間になります。
また、青のA1~B オレンジのA2~B1は波高で、シャフトのシナリ幅の大きさを表すことになります。

以上の波形図から、青シャフト オレンジシャフトの二本の機能について以下のことが解明できます。
青のシャフトは、波形から波長が短く、波高も低いため、シャフトの復元時間が早く、フェースローテイションも小さい事がわかります。
このフェースローテイションが小さいことは、ヘッドの返りが鈍い反面、インパクトでフェース向きが安定していることになります。
ヘッドスピードの速いゴルファー向き
一方、オレンジのシャフトは、波形から波長が長く、波高も高いため、シャフトの復元時間が遅く、フェースローテイションも大きくなり、シャフトが軟らかい事がわかります。 このフェースローテイションが大きい事は、インパクトでヘッドの返りが良い反面、フェース向きが不安定になることです。
ヘッドスピードの遅いゴルファー向き

右の図の様に、固有振動数の特徴は、260cpm、250cpmの波長(A~C A~C1)はサイクル運動が衰退しても波長(A~C A~C1)の復元時間は一定で変化を起こさず、波高だけが低く衰退していくのが特徴です。
ここで、重要なことは、波長が変化せず、波高のみ変化する事の意味は、図の赤円では強くスイングした時、オレンジ円は普通にスイングした時、空色はゆったり振った時、でも波長の変化は起こらず、シャフトのシナリ速度は変化しないことです。
つまり、シャフトごとに固有のタイミングを持ち、ヘッドスピードを変えることでも、このタイミングの時間は不変であることです。
これが、シャフトの持つ特性で固有振動数になります。
例えば、硬いシャフトを使用してるゴルファーが、力一杯スイングを行い、シャフトを軟らかく使おうとしても、波長の長さは一定で変化は起こりません。つまりインパクト時のタイミングの変化は起きないことです。

つまり、力一杯振ってもインパクトのタイミングが合わずスイングを崩すだけの事になります。
このように、シャフトの硬さが負荷をいくらかけても変化しない性質を固有振動数理論になります。
この様に、振動数をただ数値化するのではなく、波形を分析すれば青の260cpmとオレンジの250cpmのシャフトの波長と、波高の特性の違いがはっきりと目で確認でき理解できるようになります。
また、青シャフトが最適なゴルファーがオレンジのシャフトを使えば、インパクトのタイミングの違いや、シナリ幅の違いでフェースが暴れ正確なショットが打てない事になります。
振動数と硬さの基準
260cpmは1分間でA~C(1ヘルツ)が260cpm回起こることなります。同じように250cpmは1分間でA~C1が250回起こります。
振動数の数値が多い方がシャフトは硬く、インパクトでのフェースの開閉の可動領域が小さく操作性は良いことです。
逆に、少ない方がシャフトが軟らかくインパクトでのフェースの開閉の可動領域が大きくなり操作性は悪い事くなります。
振動数は数値の大きい方がシャフトが硬く、数値の少ない方がシャフトが軟らかいことになります。
【参考資料】
|
|
|
|---|---|
|
|
|
|
|
|---|---|
|
|
ブランド別ゴルフクラブはこちらから
メーカ別シャフト装着はクラブこちらから

ゴルフジャンル一覧と売れ筋ランキング
ゴルフクラブ |
|
|---|---|
|
|
|
|
|
|
ウエアー |
|
|---|---|
|
|
|
|
|
シューズ |
|
|---|---|
|
|
|
|
|
|
| バッグ・グローブ・ボール・その他 | のアイテム |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
人気の新作クラブ・シューズ・ウェア・バッグ・グローブ・ボール・ゴルフナビなどが大集合!レディース・メンズ・子供用も品数豊富に取り揃え。口コミ・ランキング・各種特集ページから簡単にお選びいただけます。
ラウンド中のコース戦略のための対応やクラブ選択についての情報
![]()
![]()
関連ページ
- シャフト理論の定義
- ゴルフの上達はゴルフ理論でシャフトとスイングのメカニズムを理解することから。 ゴルフ理論でクラブ選定方法、製造方法として振動数理論並びに重量管理理論を提案、平成元年に発明その後、日本で初めて特許を平成6年に取得(第2597789号)、富士通FMRシリーズゴルシスとして、大手ゴルフクラブメーカブリヂストンスポーツや、大手シャフトメーカマミヤOPに情報提供、この分野においてはパイオニアとして貢献してまいりました。その資料を基に当サイトは構成されています。
- クラブが先か?スイングが先か?
- ゴルフは18ホールをいかに少ない打数で、ボールをカップに入れるかを争うゲームです。 そこで長年に渡り議論されている、スイングが先か?道具が先か?の議論です。 もちろん、クラブもスイング共に重要であることには違いはありませんが、この議論を長年のゴルフ歴史を振り返ることで、この問題点をひも解くポイントがが見つかります
- シャフトの役割と基礎知識
- ゴルフの話題と言うとどうしてもクラブヘッドに関心が集まりますが、ゴルフクラブに大きな要素としてシャフトがあり、むしろシャフトより重要な役割を果たしているといえます。 その理由はシャフトはスイングに直接影響を与えるものだからです。ヘッドがボールに影響を与えるものであれば、シャフトはスイングを決める重大な要因になるからです。
- シャフトの重要性とメカニズム
- ヘッドスピードとシャフトの硬さの不一致は飛距離ロスや方向性を不安定にします。飛距離アップや正確なショットはミート率を上げボール初速度をあげることです。そのためにも、ヘッドスピードとシャフトの硬さを一致させる事は絶対条件です。
- シャフト選択を徹底解説
- ゴルフ上達にはクラブ選択が欠かせません。あらゆるスポ―ツ゚に科学的分析が取り入れられ道具でも目覚ましい進化が認められます。ゴルフシャフトも飛距離や方向性において画期的な進化を遂げてきました。ここでは、シャフト選択の重要なポイントを解説します。 .
- シャフト測定の問題点
- シャフトの硬さの測定には静止的測定と動的測定があります。シャフトの硬さを正確に知る事は、飛距離アップや正確なショットなど色んな悩みの原因を解決できます。それには、静止的測定の問題点が存在します。この問題点をゴルフ理論・スイング理論で科学的、物理的に理解する事でゴルフの上達は驚く程早くなります。無駄のないクラブ選択、効果的なスイング練習ができます。ノウハウなくて決して上達はありません。 .
- 固有振動と長さ、バランスの関係
- ヘッドスピードとシャフトの硬さの不一致は飛距離ロスや方向性を不安定にします。飛距離アップや正確なショットはミート率を上げボール初速度をあげることです。そのためにも、ヘッドスピードとシャフトの硬さを一致させる事は絶対条件です。
- シャフトの絶対硬度
- 絶対硬度と言う言葉は聞きなれない言葉だとおもいますが、シャフトを選択、クラブの調和には絶対必要な原理原則理論です。
- シャフトのタイミングのメカニズム
- シャフトのタイミングは直接飛距離、方向性に大きな影響をあたえます。このタイミングとはシャフトのシナリの時間であり、ヘッドスピードに比例関係にあります。シナリのメカニズムを知ることで自分に合うクラブの選択が明確になってきます。
- シャフトとヘッドスピードの一致
- ヘッドスピードとシャフトの硬さの不一致は飛距離ロスや方向性を不安定にします。飛距離アップや正確なショットはミート率を上げボール初速度をあげることです。そのためにも、ヘッドスピードとシャフトの硬さを一致させる事は絶対条件です。
- ミート効率で飛距離アップ
- 飛距離アップにはボール初速を上げることで可能になります。このボール初速を上げるにはインパクトでミート率を上げるです。ヘッドスピードが速いからと言う理由で飛距離が出ることにはならないのです。
- シャフトのスイートスポット
- ヘッドスピードとシャフトの硬さの不一致は飛距離ロスや方向性を不安定にします。飛距離アップや正確なショットはミート率を上げボール初速度をあげることです。そのためにも、ヘッドスピードとシャフトの硬さを一致させる事は絶対条件です。
- ミート効率を高めるシャフト振動数とライ角
- ヘッドスピードとシャフトの硬さの不一致は飛距離ロスや方向性を不安定にします。飛距離アップや正確なショットはミート率を上げボール初速度をあげることです。そのためにも、ヘッドスピードとシャフトの硬さ、適正なライ角を一致させる事は絶対条件です。
- シャフトの キックポイントの役割
- シャフトには振動数と共にシャフトのキックポイントとトルクがあり、ゴルフには重要なファクターです。キックポイントは弾道の高低やスイングスタイルに、トルクはインパクトのヘッドの返りに影響をあたえます。
- シャフトのトルクとヘッドスピード
- シャフトはインパクトにかけて、複雑な動きをします。 それは、シャフトの本来の性質である直進性のシナリです。このシナリはシャフトの硬さになりますが、それとば別に直進性のシナリに同調するようにシャフトにはネジレがおこります。このねじれがトルクです。
- シャフトの振動数
- シャフトはダウンスイングでヘッド重量と体の回転の加速でシナリを起こします。 このシナリは一定の固有の速度で元の状態に復元特性を持っています。 このシャフトの特性は振動数で表現できヘッドスピードに大きく関係しています。
- シャフトのシナリ
- ゴルフクラブで最も重要な役目を持っ理由は、シャフトはインパクトまでクラブを導くことです。つまり、インパクトまでの仕事はシャフトが行うことです。 シャフトのシナリは、スイングの振る速さ(ヘッドスピード)とヘッドの重さで起こるシャフトの歪みで、その歪みはパワーになります。このシナリは速度を持ち、ヘッドスピードとマッチングすることが、シナリを生かせることになるのです。
- シャフトのフレックスと振動数
- .一般的なシャフトのフレックスの決め方は、素材の硬さであって、シナリの硬さではないことです。 その素材の硬さに一定の負荷をかけた場合に、シャフトのシナリ幅(ABOUT)で決めていることです。 振動数はシャフトの素材の硬さでなく、シャフトの素材や長さで変化するシナリを測定した値です。
- スチールシャフトとカーボンシャフトの違い
- スチールシャフトとカーボンシャフトの選択は、シャフトの重さが基準になります。 スチールシャフト、カーボンシャフトのメリット、デメリットをシャフトの重さや、シャフトのシナリ、トルクから解説します。
- シャフト重量と重量フロー
- ゴルフで重要なスイングのリズムは、スイングスピードに適したクラブ重量、すなわちシャフト重量でリズムよくスイングできることになります。 クラブの構成要素の中でシャフト重量の重さが最も重要でえヘッドスピードに密接に関係してきます。 また、このシャフト重量は、ウッドとアイアンの重量フローが正しくないとリズムが狂い、ミスショットを打つ原因になるのです。
- 重いシャフトと軽いシャフトのメリット・デメリット
- シャフトはスイングを作ると言われます。 特に重さや硬さで、使用ゴルファーが異なってきます。 つまり合う、合わないがあり、詳しく解説していきます。
- シャフトを長くする、短くする
- シャフトの長さはスイングに様々な影響を及ぼします。特に、ドライバーの場合にその影響は顕著に表れ、主に飛距離や方向性に現れます。
- シャフトメーカー情報
- ゴルフクラブの心臓部はシャフトといえます。 シャフトの硬さ、重さ、トルクなど自分のスイングに合わせることが選択のポイントです。 そこで、ドライバーとアイアンの人気商品を紹介。














